Yet more Numbering Clues from 'Das Triumphans'.

I know that my continual demonstration of clues I have found in Bessler's work seem to be centred on the existence of hidden pentagrams and a few alphanumeric clues.  The usual question is, so what?  Where are the clues which will lead to constructing a replica of Bessler's wheel?  My point in advertising these seemingly  irrelevant pieces of coding is to show that Bessler wanted us to find them and provided dozens and dozens of them in various forms so that we would eventually get the message and realise that there must be more to find and that it would eventually lead to the discovery of more graphic information and subsequently his wheel.

Many of us are convinced that Bessler's claims were genuine, even though we don't know how he did it.  Assuming he was genuine then, why would he waste his time in creating so many ingenious clues in all of his publications, extolling the virtues of his wonderful machine, and include illustrations that do nothing to tell us about the machines.  Why bother? Because the coded clues are intended to provide information or at least point to where that information can be found  The number 55 rears .its head with monotonous regularity and you'd have to be blind not to see where it's pointing to - his Apologia Poetica, Chapter 55.  http://www.orffyreus.net/html/chapter_55.html  shows everything I've discovered about chpater 55 and it is obviously full of encoded material and one day someone will work out how to decipher it. I confess it has beaten me so far although I understand that there are others working on it who are optimistic that they are making some headway.

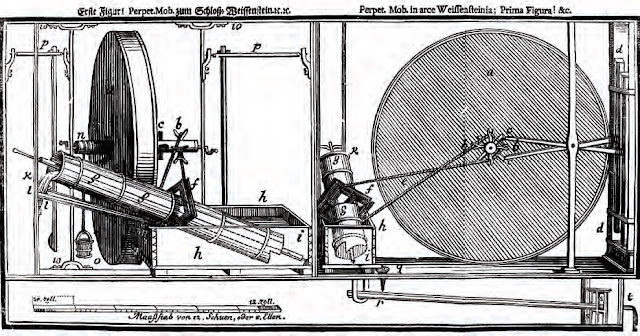
So back to the numbering clues in the Das Tri illustrations.  Johann Bessler included an illustration showing the perpetual motion machine at Schloss Weissenstein.  It was connected to an archimedes pump and apparently demonstrated its power to pump water. See the illustration below.

Like the previous one this drawing is in two parts.  It uses letters from the alphabet rather than numbers this time to label the different parts.  The letters run from  'A' to 'T', in lower case.  He has omitted the letter 'J' because as we know, it is used as an alternative to the letter, 'i' in the German 24 letter alphabet, which is present.  Curiously the letter 'W' appears twice at the top of left side drawing and once at the bottom.  I say curiously because the letters 'U' and 'V' have been omitted and yet they are alternatives to each other and one might have expected to find one of them present seeing as their following letter, 'W' is included.

But there is more.  The itemised list that accompanies this illustration includes all the lower case letters with descriptions of the parts, but then uses the number ten in place of the apparent 'W' as seen in the drawing itself.  Furthermore closer scrutiny of the hand-drawn 'W' shows that it could also be read as the number ten.  But this makes no sense since the rest are labelled alphabetically.

 

In confirmation of this see the example from the list below. The letter 's' then 't' is followed by the number '10'.

Bessler's frequent use of alpha-numerics demands that we check out the possible use of them in this illustration.  Clearly we are meant to convert all the letters to numbers. 

Adding up the subsequent numbers gives a total of 355, but this seems insignificant, until you realise that Bessler has again omitted one of the number 5s.  The number 5 identifies the rope in the right drawing but there is no such label attached to the rope in the left drawing.  From previous analyses we know that this is a typical Bessler method of encoding information within a drawing.  Adding the missing number 5 to the total brings it up to 360.

The total of numbers comes to 40 with the inclusion of the missing number 5 and as we have done before we divide 360 by 40 to give us 90.  A total of 90 again points to 18 times 5.  Once again we see the two main numbers associated with the pentagram.

As we saw in the previous drawing, the illustrations are in two halves.  Looking at the bottom of the right drawing there seem to be an unnecessary addition of extra letters, for instance there are two completely superfluous S’s and in fact the bottom of this right side drawing seems almost to have been added as an afterthought designed to boost the total to 360. See below.

Adding up the numbers in the right side drawing but excluding those extra ones underneath gives us 72, another key number in the pentagram.  The numbers in the left drawing total either 190 or 195 depending whether you include the missing number 5, but there are 18 numbers in total. The total number of letters used throughout is 20 if you count the 'W' as a letter and not a number.  360 divided by 20 equals 18. Bessler achived two things in this illustration, he demonstrated the presence of the number 72 again in the right side drawing excluding the numbers underneath - and he then obtained another meaningful number by adding both sides and including the extra numbers under the right side to get 360.  Of course 360 divided by 72 equals 5.

There are other clues buried in this illustration.  For instance in the picture below one can see two lines drawn in red, separated by a red vertical line forming angles of 72 degrees and the other, in blue, which is 54 degrees to the same vertical line, each seem to suggest another pentagram.

Back to the workshop for me now!

JC

More of Bessler's numbering clues in ‘Das Triumphans’.

After the two illustrations discussed in my previous post I have decided to offer my findings in another of the illustrations; this time the ‘Andere Figura’ and the ‘Secunda Figura in ‘Das Triumphans’.  Again I am discussing the numbering used in them.  I have placed a copy of the drawing below.  Again a single click on the picture will bring up an enlarged version so you can see the numbering more clearly.

The first thing to note in the pictures shown above, is that the right side of the left picture has been truncated slightly. In the book they are separated by a small gap filled with thin black and white lines, clearly designed to allow for the inner margins being partially enclosed by the book binding.  These lines allow you to bring the edges of the two illustrations close together as shown above.

In the drawing above you can see that the left circle can be completed and joins at the circumference of the right circle.  Notice that the circle I've drawn in, does not follow the original one as it leaves the left page.  This is due to the page being pulled inwards at the central binding which has slightly deformed the printed circle.  I always thought that the two pages were intended to be joined and I tested the theory with my original copy of  DT, by pressing the pages flat with a piece of glass and adjusting the right page until the thin black and white dividing lines were hidden.  It was then possible to draw in the complete circle to show that it did indeed abut the right circle.  As a check, note that the left half of my added circle aheres closely to the original one and that it only diverges as the bend in the paper aproaches the central crease.

In the above picture you can see yet aother pentagram inside the left picture. Notice how the extension of one of the chords of the pentagram runs through the middle of the right picture. This extension to the pentagon is governed by the close proximity of the two pictures so one must assume that the extension is intentional.  The main supporting pillar forms a perfect angle of 72 degrees with the extended chord, thus indicating the rotational angle of a second pentagon.  

I've included the additional pentagram in the above picture, which may seem more speculative and I must admite that although it looks possible, I have found it difficult to draw in a perfect pentagram so please add a pinch of salt to this particular suggestion.

In the right side picture above, the large triangular pendulum has some curious properties which seem to be additional clues.  They are 30 degrees for the bottom angle, and 78 and 72 degrees for the upper left and right angles respectively.  The 72 degree angle obviously fits in with the hidden pentagon, but is there an additional clue there?  Of course!

The second thing is that the right picture seems to have an excess of the number eight (four).  This over-labelling looks suspiciously like the same technique I have described for the two first wheel pictures.  Could this be another indication of a grand total being sought?  

Yes - the numbers in the left picture add up to 28; those in the right, 62, to total 90.  There are 15 numbers used and 90 divided by 15 is six.  But this does not seem to be a significant number, however Bessler’s favourite number 5, divides exactly 18 times into 90 – 5 and 18; the ubiquitous pentagonal numbers again.  Secondly the numbers used, 1 to 10, add up to a total of 55 – the other Bessler number. 

JC

 10a2c5d26e15f6g7h10ik12l3m6n14o14r5s17tu6v5w4y4-3,’.

Some of Bessler's Wheel numbering clues described.

This is a brief account of the odd numbering used by Bessler in labeling his two wheels, the Weissenstein one from Grundlicher Bericht and the second one the Merseberg wheel from Das Triumphans. For simplicity I shall refer to them as the W wheel and the M wheel.

By the way, click once on either illustration to get a large version to see the numbering more easily.

It becomes quite clear that some of the items are ‘over-numbered’.  By that I mean that Bessler seems to have labelled the parts with a particular number more often than one might think was necessary. For example the main pillar supporting the wheel is numbered 4, four times.  The slimmer pillars are numbered 12, and two of them to the left are numbered twice each, yet the other two are only numbered once each. Some numbers appear more often than others and not just because they are attached to more similar pieces. After number 18 the rest of the numbers are lone examples. I speculated that this was done to achieve a certain total, and having identified each part once with its number, he then sought to add to the total by labelling the same parts more than once. Obviously the higher numbers would make the jumps toward his desired total too big so he started at the lower end of the range and gradually added numbers until he had achieved his desired end.  Why he did this was unclear to me at the time.

In the W wheel there are two number 18’s yet one has been omitted in the M wheel – error or deliberate anomaly? In the W wheel the number 5 is barely visible in the box at the bottom of the sideways-on wheel, yet it has clearly been omitted in the M wheel.  In the W wheel some of the weights at the ends of the pendulums are numbered 11, there are eight of them, yet in the M wheel one of them has been omitted.  Finally in the W wheel there are two number 24’s attached to the padlocks, yet in the M wheel one of them has been reversed to become 42.  How can we explain all these anomalies?

The omission of 5 and 18 in the W wheel is explained by the fact that 5 is the most important number to Bessler because of its importance to the pentagram, and 18 degrees is the basic angle of the pentagram.  Changing the number 24 to 42 can be explained by the omission of 18, because 42 - 24 = 18.  Bessler ensured we got this information by altering the second drawing.  First he removed the 5 and an 11 (5 x 11=55).  Then he assumed that we would compare the two drawings and realize that the second one not only omitted these two numbers, but also when totalled the numbers add up to 633, whereas in the M wheel the total is 649.  But of course 633 from 649 equalled 16 (5 + 11).

In the first drawing the numbers, composed from 59 numbers, add up to 649, which is, interestingly, equal to 59 x 11 (both prime numbers).  In the second drawing the numbers add up to 633, which is 16 short of the 649.  In the second drawing the numbers 5 and one of the 11s has been omitted, which is why the second drawing does not match the 649 of the first drawing.  In both drawings the picture cuts off the left hand end of the drawing and in the process cuts off one of the number 11 weights.  If, in the first drawing, this is added to the 649 of the first drawing it produces the number 660, and because we then have 60 numbers, 660 divided by 60 equals 11, but more interestingly, 660 divided by 12 equals 55!  The same applies to the second drawing but you have to add the extra eleven to make 660.

JC

 10a2c5d26e15f6g7h10ik12l3m6n14o14r5s17tu6v5w4y4-3,’.