I know that my continual demonstration of clues I have found in Bessler's work seem to be centred on the existence of hidden pentagrams and a few alphanumeric clues. The usual question is, so what? Where are the clues which will lead to constructing a replica of Bessler's wheel? My point in advertising these seemingly irrelevant pieces of coding is to show that Bessler wanted us to find them and provided dozens and dozens of them in various forms so that we would eventually get the message and realise that there must be more to find and that it would eventually lead to the discovery of more graphic information and subsequently his wheel.
Many of us are convinced that Bessler's claims were genuine, even though we don't know how he did it. Assuming he was genuine then, why would he waste his time in creating so many ingenious clues in all of his publications, extolling the virtues of his wonderful machine, and
include illustrations that do nothing to tell us about the machines. Why
bother? Because the coded clues are intended to provide
information or at least point to where that information can be found The number 55 rears .its head with monotonous regularity and you'd have to be blind not to see where it's pointing to - his Apologia Poetica, Chapter 55. http://www.orffyreus.net/html/chapter_55.html shows everything I've discovered about chpater 55 and it is obviously full of encoded material and one day someone will work out how to decipher it. I confess it has beaten me so far although I understand that there are others working on it who are optimistic that they are making some headway.
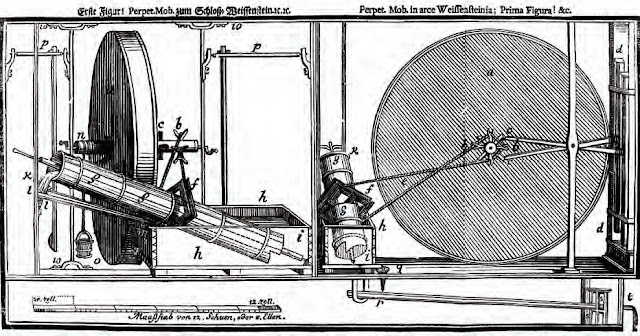
So back to the numbering clues in the Das Tri illustrations. Johann Bessler included an illustration showing the perpetual motion machine at Schloss Weissenstein. It was connected to an archimedes pump and apparently demonstrated its power to pump water. See the illustration below.
Like the previous one this drawing is in two parts. It uses letters from the alphabet rather than numbers this time to label the different parts. The letters run from 'A' to 'T', in lower case. He has omitted the letter 'J' because as we know, it is used as an alternative to the letter, 'i' in the German 24 letter alphabet, which is present. Curiously the letter 'W' appears twice at the top of left side drawing and once at the bottom. I say curiously because the letters 'U' and 'V' have been omitted and yet they are alternatives to each other and one might have expected to find one of them present seeing as their following letter, 'W' is included.
But there is more. The itemised list that accompanies this illustration includes all the lower case letters with descriptions of the parts, but then uses the number ten in place of the apparent 'W' as seen in the drawing itself. Furthermore closer scrutiny of the hand-drawn 'W' shows that it could also be read as the number ten. But this makes no sense since the rest are labelled alphabetically.
In confirmation of this see the example from the list below. The letter 's' then 't' is followed by the number '10'.
Bessler's frequent use of alpha-numerics demands that we check out the possible use of them in this illustration. Clearly
we are meant to convert all the letters to numbers.
Adding up the subsequent numbers gives a total of 355, but this seems
insignificant, until you realise that Bessler has again omitted one of the
number 5s. The number 5 identifies the
rope in the right drawing but there is no such label attached to the rope in
the left drawing. From previous analyses
we know that this is a typical Bessler method of encoding information within a
drawing. Adding the missing number 5 to
the total brings it up to 360.
The total of numbers comes to 40 with the inclusion of the
missing number 5 and as we have done before we divide 360 by 40 to give us
90. A total of 90 again points to 18 times 5. Once again we see
the two main numbers associated with the pentagram.
As we saw in the previous drawing, the illustrations are
in two halves. Looking at the bottom of
the right drawing there seem to be an unnecessary addition of extra letters,
for instance there are two completely superfluous S’s and in fact the bottom of
this right side drawing seems almost to have been added as an afterthought designed to
boost the total to 360. See below.
Adding up the numbers in the right side drawing but excluding those extra ones underneath gives us 72, another key number in the pentagram. The numbers in the left drawing total either 190 or 195
depending whether you include the missing number 5, but there are 18 numbers in total. The total number of letters used throughout is 20 if you count the 'W' as a letter and not a number. 360 divided by 20 equals 18. Bessler achived two things in this illustration, he demonstrated the presence of the number 72 again in the right side drawing excluding the numbers underneath - and he then obtained another meaningful number by adding both sides and including the extra numbers under the right side to get 360. Of course 360 divided by 72 equals 5.
There are other clues buried in this illustration. For instance in the picture below one can see
two lines drawn in red, separated by a red vertical line forming angles of 72 degrees and the other, in blue, which is 54
degrees to the same vertical line,
each seem to suggest another pentagram.
JC