1) As planned I’m sharing information both here and on the Besslerwheel.com forum Besslerwheel forum . So here is the first part. All of the clues originate from the drawings and text in Grundlicher Bericht, Apologia Poetica, Das Triumphirende and Maschinen Tractate. I will try to keep the details brief and to the point so I won’t be showing where and how I obtained the answers but you can probably work out some of them.
I have always thought that there were two hard facts established about the internal workings of Bessler's wheel and one of them was that there were five mechanisms. The other was that the weights worked in pairs. All else is open to conjecture. But one certainty is that Bessler thought that this piece of information was extremely important and even encoded it in his name right from the moment he adopted the pseudonym, Orffyreus.
I’m well aware that many people dismiss my belief that Bessler used five mechanisms in his wheel but in fact I would go further than that and state that he designed wheels which all had an odd number of mechanism. In [i]Maschinen Tractate (MT)[/i] he suggested this with the following number system, see below:-
He identifies the odd numbers as you see by placing a ‘Z’ next to the odd numbers to provide a clue. There are other clues offering the same information that he used 5, 7 and 9 mechanisms.
The plethora of references to the number five also include a number of pointers to the pentagram. The geometric figure is embedded in many drawings and I’ll show one below. Bessler was familiar with the books by Euclid and in this case he referred to Euclid’s 11th proposition, which ran thus::-
“To inscribe an equilateral and equiangular pentagon in a given circle….”
….and his alternative method, and note how the red and blue lines are designed to skim the edges of the two inner circles. Finally the white angles are 24 degrees. 24 x 3 = 72, 5 x 72 = 360.
JEEB using the Caesar shift becomes WRRO. R is the 18th letter. W 23rd letter which may only be there for the following reason, W is composed of two Roman numerals, V meaning 5.
He often, (dozens of times) hand wrote the letter W as shown below, as two Roman numerals linked together, and you can see it twice in the accompanying passage. They are linked to point to them as pairing, but not in the same 5th segment of the wheel.
Bessler used any opportunity to put a veiled reference to these numbers. I should also point out that the 2G’s, refers to his enemy in chief Andreas Gärtner. The 2 W’s refers to another enemy, Christian Wagner, the two B’s refer to the third enemy, Johann Gottfried Borlach.
First there are the four numbers added to the bottom left corner - 138, 139, 140 and 141. Was Bessler trying to reach the number 141 to get the only factors. 3 x 47, which might link to the three images on MT47?
Was he pointing to Euclid’s 47th construction i.e, “in any right triangle, the square of the two sides connected to the right angle is equal to the square of the third side called the hypotenuse?” Also known as the 3-4-5 right angle?
Or was it the total of 558? 558 seems meaningless unless you simply add them together to get 18. 18 being the basic number upon which all the others are multiples of, in the pentagram, thus number 5 again.
Secondly there is the carefully drawn number 5. placed near to the comment about children’s games. The fact that it has full stop or period with it means it’s a standalone clue or hint, it doesn’t really relate to the number of children’s games. This is also linked to the pentagram.
Thirdly the figures in the Toys page can be divided by 5, see the image below.
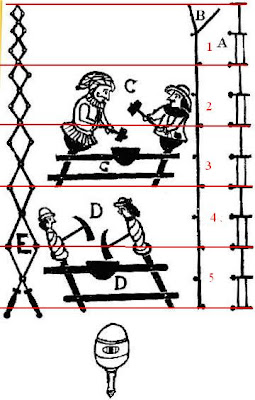
Bessler says (paraphrased) that the weights work in pairs. That means one weight from each of two adjoining segments work together, but only when they are at the lowest point in rotation. This will be shown to be part of Bessler’s “connectedness principle”, but there is more to know about that.
The reason for the inclusion of figures C and D is that they form a pair at each advance in rotation of one fifth. When C falls, it pulls D back up a little.
The second figure D, has no arms so although it has weights i.e. an axe, it cannot move of itself, because it has already fallen - so has to be moved by another similar figure, i.e. figure C. Note that figure D has spirals around its body, this is to show that it lies at a different angle to figure C, because it is in the adjacent 5th segment. There is a length of cord running between each of the figures in A, when the active figure C, falls, he pulls the inactive fallen figure D upwards towards its former position.
One of Bessler’s asides includes the following:- a great craftsman would be he who, as one pound falls a quarter, causes four pounds to shoot upwards four quarters.”