The pentagon shown in the previous blogs is inverted and concerns have been raised about the evil connotations associated with this figure, so you will doubtless be pleased to discover that perhaps Bessler was also concerned, because he left information about how to rotate it to a more virtuous position, although not necessarily for reasons connected with his soul.
I’m jumping the gun a bit here but to calm those God fearing souls who are worried about my publishing an inverted pentagram, I am posting some information earlier than I originally intended to.
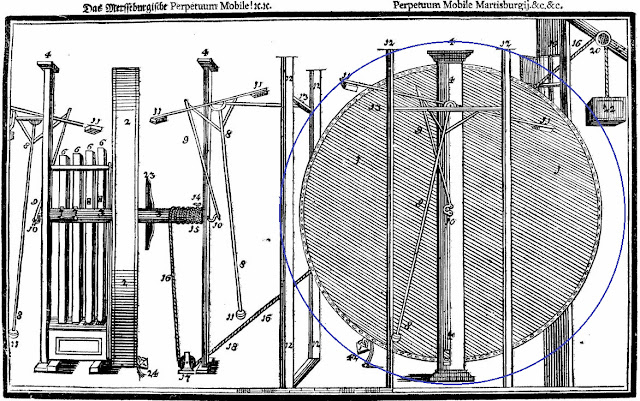
The Merseburg illustration contains a list of numbered parts. The numbers run from 1 to 24, as was used in the original version of the illustration printed in his first publication Gruendlicher Bericht (GB), but in his later version, the padlock which should be numbered 24 seems to have got its numbers the wrong way round, it reads 42.
For those who think it’s a typo, rest assured, it isn’t. Apart from the fact that printing from a wood block, or woodcut, requires skill and patience and the result is checked throughout to ensure accuracy, the numbers in both illustrations add up to 660 for reasons to be explained shortly, which means that he must have removed a number 18 in the second version to retain the same total, and that is what he did. See the illustration below to see how and why,
The red line shows the path of the rope as it passes behind the wheel, and also indicates the starting place to obtain the pentagon. The green line runs from the point on the padlock up to the point where the top end of the red line crosses the edge of the wheel. The numbers on the padlock need to be rotated to read 24 and the green line should also be rotated 180 degrees. This rotates the pentagon too.
In the illustration the inverted pentagon is shown in yellow, and the upright one is shown in blue. Notice that it is still slightly tilted to the left, for reasons which will become clear later.
Sorry this is a short blog, but I’m very busy working to finish my wheel.,
NB. I'm adding a brief explanation of the number anomalies found in the drawings in GB and DT because I did not explain my reasoning in the above blog due to lack of time
Bear in mind that Bessler wanted to provide clues but we have to work at explaining some of them, and he also usually provided more than one way of discovering his intentions. So here goes:-
In GB the items are numbered from 1 to 24, in DT they are also numbered 1 to 24, plus the lone
number 42. This looks like a simple printing error but of course I have always maintained that
Bessler deliberately introduced such anomalies as clues. I’ll discuss this one later, first we need to
look at some of the features apparent in the numbering.
It becomes quite clear that some of the items are ‘over-numbered’. By that I mean that Bessler
seems to have labelled the parts with a particular number more often than one might think was
necessary. For example the main pillar supporting the wheel is numbered 4, four times. The
slimmer pillars are numbered 12, and two of them to the left are numbered twice each, yet the
other two are only numbered once each. Some numbers appear more often than others and not
just because they are attached to more similar pieces. After number 18 the rest of the numbers are
lone examples. I speculated that this was done to achieve a certain total, and having identified each
part once with its number, he then sought to add to the total by labelling the same parts more than
once. Obviously the higher numbers would make the jumps toward his desired total too big so he
started at the lower end of the range and gradually added numbers until he had achieved his
desired end.
The numbers in GB total 649 and those in DT 633 - not apparently significant, but let’s look more
closely.
In GB there are two number 18’s yet one has been omitted in DT. In GB the number 5 is barely
visible in the box at the bottom of the sideways-on wheel, yet it has clearly been omitted in DT. In
GB the weights at the ends of the pendulums are numbered 11, there are eight of them, yet in DT
one of them has been omitted. Finally in GB there are two number 24’s attached to the padlocks,
yet in DT one of them has been reversed to become 42. Its almost impossible to see but in the first
drawing, GB, the second number 18 is almost invisible, having been squeezed into the small hole
through which the rope is supposed to pass. It is undoubtedly not there in DT. How can we explain
all these anomalies?
The omission of 5 and 18 in DT is explained by the fact that 5 is the most important number to
Bessler because of its connection with the pentagram, and 18 degrees is the basic angle of the
pentagram. Changing the number 24 to 42 can be explained by the omission of 18, because 42 - 24
= 18. He might have done this because of the difficulty of identifying both the the 5 and the second
18 in GB, and this lends credence to the idea that the numbers must add up to something
significant. Of course I have offered an explanation for the reversed numberr 24 in my blog above.
Bessler ensured we got this information by altering the second drawing. First he removed the 5
altogether plus he omitted one of the 11s, and 5 x 11=55. Then he assumed that we would
compare the two drawings and realize that the second one not only omitted these two numbers, but
also when totalled, the numbers add up to 633, and 633 from 649, the total of the numbers in GB,
equalled 16 (or 5 + 11). As we know, 55 figures abundantly through out Bessler's works.
So, in the first drawing (GB) the numbers, composed from 59 numbers, add up to 649, which is,
interestingly, equal to 59 x 11 (both prime numbers). In the second drawing (DT) the numbers add
up to 633, which is 16 short of the 649. In the second drawing the numbers 5 and one of the 11s
has been omitted, which is why the second drawing does not match the 649 of the first drawing. In
both drawings the picture cuts off the left hand end of the drawing and in the process cuts off one
of the number 11 weights. If, in the first drawing, this is added to the 649 of the first drawing it
produces the number 660, and because we then have 60 numbers, 660 divided by 60 equals 11,
but more interestingly, 660 divided by 12 equals 55! How do we know that he intended us to figure
this out? Because in both drawings there is an additional geometric feature which confirms it. The clock I described in my blog in 3 September 2016
I had noticed early on that the perspectives used in both drawings ran through the centre of the
main wheel, and I just assumed that this was done from an artistic viewpoint. However I had
already drawn all these lines in by extending them from one side to the other, in the process of
which I noticed that there were twelve lines, marking out the face of a clock. I had wondered if this
was deliberate but now I knew why it had been done. Twelve to six, three to nine, one to seven,
eleven to five and ten to four all followed lines of perspective.
To cinch the argument, the only one that did not, was two to eight o’clock, but interestingly the line
exactly lined up the number eights attached to the weights, and there were two of them. That line
defined the eight o’clock line.
So extending all the perspective lines available to us, which cross in the centre of the wheel,
provides us with a clock face. Using this we can divide up the picture and therefore the numbers by
twelve. To recap, in the first drawing,649 = 59 x 11; add the missing 11, making 660 (60 x 11) the
clock hints at 12, and 660/12=55! In the second drawing we can do the same - 633 + the missing
5 and the 11, plus the other 11 from the left side of the picture = 660. 660 divided by the twelve
equals 55.
I hope this clears up any confusion?
I’ve just added a clearer picture if the GB wheel.
JC
Copyright © 2020 John Collins